对一些经典题目类型进行总结.比如双指针,滑动窗口,回溯,深搜广搜,动态规划,贪心等等
数组
数组有时会出一些挺有意思的题
有多少小于当前数字的数字
给你一个数组 nums,对于其中每个元素 nums[i],请你统计数组中比它小的所有数字的数目。
换而言之,对于每个 nums[i] 你必须计算出有效的 j 的数量,其中 j 满足 j != i 且 nums[j] < nums[i] 。以数组形式返回答案。
利用一个哈希表(数组)存储值以及对应在排序数组中的索引,也就是小于它的值的个数.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
vector<int> smallerNumbersThanCurrent(vector<int>& nums) {
int sz = nums.size();
// 升序
vector<int> vec = nums;
sort(vec.begin(),vec.end());
// 元素下标相当于小于当前值的个数
vector<int> hash(101); //存储数值与的对应的位置的映射
for(int i = sz-1;i>=0;i--) {
// hash存储小于hash[i]的值的个数
hash[vec[i]] = i; // 从后向前遍历 遇到相同值 存储更小的索引
}
vector<int> result;
for(int i = 0;i<sz;i++) {
result.push_back(hash[nums[i]]);
}
return result;
}
};
有效的山脉数组
给定一个整数数组 arr,如果它是有效的山脉数组就返回 true,否则返回 false。
让我们回顾一下,如果 arr 满足下述条件,那么它是一个山脉数组:
arr.length >= 3- 在
0 < i < arr.length - 1条件下,存在i使得:arr[0] < arr[1] < ... arr[i-1] < arr[i]arr[i] > arr[i+1] > ... > arr[arr.length - 1]
1 | class Solution { |
独一无二的出现次数
给你一个整数数组 arr,如果每个数的出现次数都是独一无二的,就返回 true;否则返回 false。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
bool uniqueOccurrences(vector<int>& arr) {
int count[2001] = {0}; // 统计数字出现的频率
for (int i = 0; i < arr.size(); i++) {
count[arr[i] + 1000]++;
}
bool fre[1001] = {false}; // 看相同频率是否重复出现
for (int i = 0; i <= 2000; i++) {
if (count[i]) {
if (fre[count[i]] == false) fre[count[i]] = true;
else return false;
}
}
return true;
}
};
移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
void moveZeroes(vector<int>& nums) {
// 双指针
int sz = nums.size();
int ptr{};
for(int i = 0;i<sz;i++) {
// 遇到非零值进行交换
if(nums[i]!=0) {
swap(nums[ptr],nums[i]);
ptr++;
}
}
}
};
移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。
假设 nums 中不等于 val 的元素数量为 k,要通过此题,您需要执行以下操作:
- 更改
nums数组,使nums的前k个元素包含不等于val的元素。nums的其余元素和nums的大小并不重要。 - 返回
k。
1 | class Solution { |
旋转数组
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数1
2
3
4
5
6
7
8
9
10
11
12class Solution {
public:
void rotate(vector<int>& nums, int k) {
// 右旋数组
int sz = nums.size();
k = k%sz;
// 通过翻转字符串
reverse(nums.begin(),nums.end());
reverse(nums.begin(),nums.begin()+k);
reverse(nums.begin()+k,nums.end());
}
};
寻找数组的中心下标
给你一个整数数组 nums ,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -11
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int pivotIndex(vector<int>& nums) {
// 前缀和
int sz = nums.size();
int sum = accumulate(nums.begin(), nums.end(), 0);
vector<int> prefixSum(sz);
// prefixSum[i]表示截止到nums[i-1]的值的和
for (int i = 1; i < sz; i++) {
prefixSum[i] = prefixSum[i - 1] + nums[i - 1];
}
for (int i = 0; i < sz; i++) {
// (sum-nums[i]) == 2*prefixSum[i]
if(prefixSum[i]*2 == sum-nums[i]) {
return i;
}
}
return -1;
}
};
在排序数组中查找元素的第一个和最后一个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49class Solution {
public:
int find_first_index(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1;
int leftIdx = -2;
while (left <= right) {
int mid = (right - left) / 2 + left;
int num = nums[mid];
// 要找左边界
if (target > num) {
// 在右边区
left = mid + 1;
} else {
right = mid - 1;
leftIdx = right;
}
}
return leftIdx;
}
int find_last_index(vector<int>& nums, int target) {
int left = 0, right = nums.size() - 1;
int rightIdx = -2;
while (left <= right) {
int mid = (right - left) / 2 + left;
int num = nums[mid];
// 要找右边界
if (target >= num) {
// 右边区
left = mid + 1;
rightIdx = left;
} else {
right = mid - 1;
}
}
return rightIdx;
}
vector<int> searchRange(vector<int>& nums, int target) {
int l = find_first_index(nums, target);
int r = find_last_index(nums, target);
if (l == -2 || r == -2) {
return {-1, -1};
}
if (r - l > 1) {
return {l + 1, r - 1};
}
return {-1, -1};
}
};
链表
两两交换链表中的节点
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
ListNode* swapPairs(ListNode* head) {
if(!head) {
return nullptr;
}
ListNode* dummy = new ListNode(0,head);
ListNode* cur = head;
ListNode* prev = dummy;
while(cur && cur->next) {
ListNode* next_node = cur->next;
cur->next = next_node->next;
next_node->next = cur;
prev->next = next_node;
// 更新节点
prev = cur;
cur = cur->next;
}
return dummy->next;
}
};
回文链表
给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution {
public:
ListNode* reverseList(ListNode* node) {
ListNode* prev = nullptr;
while(node) {
ListNode* next_node = node->next;
node->next = prev;
prev = node;
node = next_node;
}
return prev;
}
bool isPalindrome(ListNode* head) {
// 走到中间然后翻转链表进行对比
if(!head) {
return true;
}
ListNode* cur = head;
ListNode* slowPtr = head,*fastPtr = head; // 双指针
while(fastPtr && fastPtr->next) {
fastPtr = fastPtr->next->next;
slowPtr = slowPtr->next;
}
// 翻转链表
ListNode* r = reverseList(slowPtr);
while(r && cur) {
if(r->val != cur->val) {
return false;
}
r = r->next;
cur = cur->next;
}
return true;
}
};
重排链表
给定一个单链表 L 的头节点 head ,单链表 L 表示为:1
L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为:1
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换
注意到目标链表即为将原链表的左半端和反转后的右半端合并后的结果。
这样我们的任务即可划分为三步:
找到原链表的中点。可以使用快慢指针来 O(N) 地找到链表的中间节点。
将原链表的右半端反转。我以使用迭代法实现链表的反转。将原链表的两端合并。因为两链表长度相差不超过 1,因此直接合并即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56class Solution {
public:
ListNode* getMiddle(ListNode* node) {
if (!node) {
return nullptr;
}
ListNode *slowPtr = node, *fastPtr = node;
while (fastPtr && fastPtr->next && fastPtr->next->next) {
slowPtr = slowPtr->next;
fastPtr = fastPtr->next->next;
}
ListNode* result = slowPtr->next;
slowPtr->next = nullptr;
return result;
}
ListNode* reverse(ListNode* node) {
if (node == nullptr) {
return nullptr;
}
ListNode* prev = nullptr;
while (node) {
ListNode* next_node = node->next;
node->next = prev;
prev = node;
node = next_node;
}
return prev;
}
void reorderList(ListNode* head) {
// 1. 先找到中间节点
ListNode* middleNode = getMiddle(head);
// 2. 翻转
ListNode* rlist = reverse(middleNode);
// 3.合并
ListNode* cur = head;
ListNode* llist = head->next;
int cnt{1};
while (rlist && llist) {
if (cnt % 2) {
cur->next = rlist;
rlist = rlist->next;
} else {
cur->next = llist;
llist = llist->next;
}
cnt++;
cur = cur->next;
}
if (llist) {
cur->next = llist;
}
if (rlist) {
cur->next = rlist;
}
}
};
环形链表
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
bool hasCycle(ListNode *head) {
ListNode* fast = head;
ListNode* slow = head;
while(fast != NULL && fast->next != NULL) {
slow = slow->next;
fast = fast->next->next;
// 快慢指针相遇,说明有环
if (slow == fast) return true;
}
return false;
}
};
环形链表II
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25class Solution {
public:
ListNode* detectCycle(ListNode* head) {
if (!head) {
return nullptr;
}
ListNode* slowptr = head;
ListNode* fastptr = head;
while (fastptr && fastptr->next) {
slowptr = slowptr->next;
fastptr = fastptr->next->next;
if (slowptr == fastptr) {
ListNode* cur = head;
// 从开头开始移动直到与slowptr相同
while (cur != slowptr) {
cur = cur->next;
slowptr = slowptr->next;
}
return cur;
}
}
return nullptr;
}
};
相交链表
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null1
2
3
4
5
6
7
8
9
10
11
12
13
14
15class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if (headA == nullptr || headB == nullptr) {
return nullptr;
}
ListNode *pA = headA, *pB = headB;
while (pA != pB) {
pA = pA == nullptr ? headB : pA->next;
pB = pB == nullptr ? headA : pB->next;
}
return pA;
}
};
双指针
滑动窗口和双指针 - LeetBook - 力扣(LeetCode)全球极客挚爱的技术成长平台
滑动窗口
循环不变量:「循环不变量」不是很高深的概念,在「算法」和「数据结构」的世界里,到处都有它的身影。「循环不变量」是指我们在编写代码的过程中,要一直循序不变的性质,这样的性质是根据要解决的问题,由我们自己定义的。「循环不变量」是我们写对一个问题的基础,保证了在「初始化」「循环遍历」「结束」这三个阶段相同的性质,使得一个问题能够被正确解决
同向交替移动的两个变量 固定长度的滑动窗口
可获得的最大点数
几张卡牌 排成一行,每张卡牌都有一个对应的点数。点数由整数数组 cardPoints 给出。
每次行动,你可以从行的开头或者末尾拿一张卡牌,最终你必须正好拿 k 张卡牌。
你的点数就是你拿到手中的所有卡牌的点数之和。
给你一个整数数组 cardPoints 和整数 k,请你返回可以获得的最大点数。
逆向思维
1 | class Solution { |
将x减到0的最小操作数
给你一个整数数组 nums 和一个整数 x 。每一次操作时,你应当移除数组 nums 最左边或最右边的元素,然后从 x 中减去该元素的值。请注意,需要 修改 数组以供接下来的操作使用。
如果可以将 x 恰好 减到 0 ,返回 最小操作数 ;否则,返回 -1 。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32class Solution {
public:
int minOperations(vector<int>& nums, int x) {
int sz = nums.size();
int sum_val = accumulate(nums.begin(), nums.end(), 0);
int target = sum_val - x;
if (target == 0) {
return sz;
}
// 滑动窗口
int val{};
int i{};
int ops = -1;
for (int j = 0; j < sz; j++) {
val += nums[j];
if (val > target) {
while (i < j && val > target) {
val -= nums[i];
i++;
}
}
if (val == target) {
ops = max(ops, j - i + 1);
}
}
if (ops == -1) {
return -1;
} else {
return sz - ops;
}
}
};
非逆向解法1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
public:
int minOperations(vector<int>& nums, int x) {
int sz = nums.size();
int sum_val = accumulate(nums.begin(), nums.end(), 0);
if (sum_val < x) {
return -1;
}
int left{}, right{};
// left指针左边代表操作的数
// right指针右边代表操作的数
int ans{INT_MAX};
while (right < sz) {
sum_val -= nums[right];
while (sum_val < x) {
sum_val += nums[left];
left++;
}
if (sum_val == x) {
ans = min(ans, sz - (right - left + 1));
}
right++;
}
if (ans == INT_MAX) {
return -1;
} else {
return ans;
}
}
};
每种字符至少取1个
给你一个由字符 'a'、'b'、'c' 组成的字符串 s 和一个非负整数 k 。每分钟,你可以选择取走 s 最左侧 还是 最右侧 的那个字符。你必须取走每种字符 至少 k 个,返回需要的 最少 分钟数;如果无法取到,则返回 -11
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class Solution {
public:
int takeCharacters(string s, int k) {
// 最长的滑动窗口长度
int sz = s.size();
// 维护最左指针和最右指针
// 左指针表示左边区域选择 右指针右边选择
vector<int> cnt(3);
for (auto& ch : s) {
cnt[ch - 'a']++;
}
int ans{INT_MAX};
if (cnt[0] >= k && cnt[1] >= k && cnt[2] >= k) {
ans = min(ans, sz);
} else {
return -1;
}
int left{}, right{};
int l{};
// [l,r]表示滑动窗口 均包含
for (int r = 0; r < sz; r++) {
// 移动右指针
cnt[s[r] - 'a']--;
while (l < r && (cnt[0] < k || cnt[1] < k || cnt[2] < k)) {
cnt[s[l] - 'a']++;
l++;
}
if (cnt[0] >= k && cnt[1] >= k &&cnt[2] >= k) {
ans = min(ans, sz -(r-l+1));
}
}
return ans;
}
}
不定长度的滑动窗口
有一类数组上的问题,需要使用两个指针变量(我们称为左指针和右指针),同向、交替向右移动完成任务。这样的过程像极了一个窗口在平面上滑动的过程,因此我们将解决这一类问题的算法称为「滑动窗口」问题。掌握好这一类「滑动窗口」的问题,需要先从「暴力解法」开始分析,「滑动窗口」利用了问题本身的特点,在两个指针同向、交替向右移动的过程中,少考虑了很多「暴力解法」需要考察了情况,将时间复杂度降到了线性级别
写对「滑动窗口」除了要弄清楚为什么可以使用滑动窗口,还需要明白代码编写过程中的「循环不变量」,这样才不会在初始化和一些边界问题上出错。我们会在例题讲解的部分和大家进行说明。
最小覆盖子串
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “” 。
注意:如果 s 中存在这样的子串,我们保证它是唯一的答案。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44class Solution {
public:
string minWindow(string s, string t) {
vector<int> cnt(256);
vector<bool> exists(256);
int counts = t.size(); // 有效字符数
for (auto& ch : t) {
cnt[ch]++;
exists[ch] = true;
}
int l{};
int min_l{}, min_len{INT_MAX};
// 维护滑动窗口[i,j] 包含的字符数
for (int j = 0; j < s.size(); j++) {
char ch = s[j];
if (exists[ch]) {
cnt[ch]--;
// 如果存在该字符
if (cnt[ch] >= 0) {
counts--;
}
while (counts == 0) {
if (min_len > j - l + 1) {
min_l = l;
min_len = j - l + 1;
}
// 满足条件 移动左指针
if (exists[s[l]]) {
cnt[s[l]]++;
if (cnt[s[l]] > 0) {
counts++;
}
}
l++;
}
}
}
if (min_len == INT_MAX) {
return "";
} else {
return s.substr(min_l, min_len);
}
}
};
替换后的最长重复字符
给你一个字符串 s 和一个整数 k 。你可以选择字符串中的任一字符,并将其更改为任何其他大写英文字符。该操作最多可执行 k 次。
在执行上述操作后,返回 包含相同字母的最长子字符串的长度。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int characterReplacement(string s, int k) {
// 滑动窗口
int sz = s.size();
int i{},j{};
int max_cnt{};
unordered_map<int,int> umap;
int res{};
while(j<sz) {
umap[s[j]]++;
max_cnt = max(max_cnt,umap[s[j]]);
while(j-i+1>max_cnt+k) {
umap[s[i]]--;
i++;
}
res = max(res,j-i+1);
j++;
}
return res;
}
};
最长湍流子数组
给定一个整数数组 arr ,返回 arr 的 最大湍流子数组的长度 。
如果比较符号在子数组中的每个相邻元素对之间翻转,则该子数组是 湍流子数组 。
更正式地来说,当 arr 的子数组 A[i], A[i+1], …, A[j] 满足仅满足下列条件时,我们称其为湍流子数组:
若 i <= k < j :
当 k 为奇数时, A[k] > A[k+1],且
当 k 为偶数时,A[k] < A[k+1];
或 若 i <= k < j :
当 k 为偶数时,A[k] > A[k+1] ,且
当 k 为奇数时, A[k] < A[k+1]。
K连续位的最小翻转次数
给定一个二进制数组 nums 和一个整数 k 。
k位翻转 就是从 nums 中选择一个长度为 k 的 子数组 ,同时把子数组中的每一个 0 都改成 1 ,把子数组中的每一个 1 都改成 0 。
返回数组中不存在 0 所需的最小 k位翻转 次数。如果不可能,则返回 -1 。
子数组 是数组的 连续 部分。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49class Solution {
public:
int minKBitFlips(vector<int>& nums, int k) {
int n = nums.size();
int ans = 0;
int active_flips = 0; // 记录当前位置 i 受到多少次活跃翻转的影响
// 遍历数组, i 代表当前窗口的起始点
for (int i = 0; i < n; ++i) {
// 1. 移除 i-K 处翻转的影响
// 如果 i >= k 且 nums[i-k] == 2 (2是我们标记的翻转起点),
// 说明从 i-K 开始的翻转已经结束,需要将 active_flips 减 1。
if (i >= k && nums[i - k] == 2) {
active_flips--;
}
// 2. 判断当前位 (i) 的实际值
// 实际值 = nums[i] XOR (active_flips % 2)
// 如果 active_flips 是偶数,实际值就是 nums[i]。
// 如果 active_flips 是奇数,实际值就是 nums[i] 的反转。
// 翻转后的状态 (0 或 1)
int current_state = nums[i];
if (active_flips % 2 != 0) {
current_state = 1 - nums[i]; // 如果奇数次翻转,则状态反转
}
// 3. 贪心决策:如果当前位实际为 0,必须从 i 开始翻转
if (current_state == 0) {
// 检查是否可以进行 K 位翻转
if (i + k > n) {
return -1; // 剩余元素不足 K 个,无法完成
}
// 执行翻转操作 (逻辑上)
ans++;
active_flips++;
// 使用 2 作为标记,表示 "从 i 开始了一次翻转"
// 并且将 nums[i] 的原始值(0或1)覆盖,因为我们不再需要它的原始值
// 后续只需要根据 active_flips 的变化来判断翻转是否结束。
nums[i] = 2;
}
}
return ans;
}
};
找出第 k 小的距离对
1 | class Solution { |
差分数组
差分数组是一种用于高效处理区间更新操作的数据结构。它本身不是一个独立的数据结构,而是一种基于前缀和思想的数组技巧或数学工具。差分数组是前缀和的逆运算。
它通过将对原始数组 $A$ 的区间修改操作,转化为对差分数组 $D$ 的单点修改操作,从而将时间复杂度从 $O(N)$ 降到 $O(1)$。
对原始数组 $A$ 的区间 $[L, R]$ 增加 $C$ 的操作,只需要对差分数组 $D$ 进行两次单点修改:
- $D[L] \mathrel{+}= C$
- $D[R+1] \mathrel{-}= C$
这两次操作的时间复杂度是 $\mathbf{O(1)}$。
会议室
给定一个会议时间安排的数组 intervals ,每个会议时间都会包括开始和结束的时间 intervals[i] = [starti, endi] ,请你判断一个人是否能够参加这里面的全部会议。1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
bool canAttendMeetings(vector<vector<int>>& intervals) {
sort(intervals.begin(),intervals.end());
// 是否有重叠区间
for(int i = 1;i<intervals.size();i++) {
if(intervals[i][0]<intervals[i-1][1]) {
return false;
}
}
return true;
}
};
会议室II
给你一个会议时间安排的数组 intervals ,每个会议时间都会包括开始和结束的时间 intervals[i] = [starti, endi] ,返回 所需会议室的最小数量 。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
int minMeetingRooms(vector<vector<int>>& intervals) {
int sz = intervals.size();
vector<int> in(sz);
vector<int> out(sz);
for(int i = 0;i<sz;i++) {
in[i] = intervals[i][0];
out[i] = intervals[i][1];
}
sort(in.begin(),in.end());
sort(out.begin(),out.end());
int usedRooms{};
int i{},j{};
while(i<sz){
if(in[i]>=out[j]) {
// 开始时间大于结束时间 重用
j++;
}else{
usedRooms++;
}
i++;
}
return usedRooms;
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39class Solution {
public:
int minMeetingRooms(vector<vector<int>>& intervals) {
int sz = intervals.size();
vector<pair<int, int>> timestamps;
for (auto& interval : intervals) {
timestamps.emplace_back(interval[0], 1);
timestamps.emplace_back(interval[1], -1);
}
sort(timestamps.begin(), timestamps.end());
int maxRooms{};
int res{};
for (auto& p : timestamps) {
maxRooms += p.second;
res = max(res, maxRooms);
}
return res;
// vector<int> in(sz);
// vector<int> out(sz);
// for(int i = 0;i<sz;i++) {
// in[i] = intervals[i][0];
// out[i] = intervals[i][1];
// }
// sort(in.begin(),in.end());
// sort(out.begin(),out.end());
// int usedRooms{};
// int i{},j{};
// while(i<sz){
// if(in[i]>=out[j]) {
// // 开始时间大于结束时间 重用
// j++;
// }else{
// usedRooms++;
// }
// i++;
// }
// return usedRooms;
}
};
会议室III
花期内花的数目
拼车
1 | class Solution { |
栈与队列
花括号展开
给定一个表示单词列表的字符串 s 。单词中的每个字母都有一个或多个选项。
- 如果有一个选项,则字母按原样表示。
- 如果有多个选项,则用大括号分隔选项。例如,
"{a,b,c}"表示选项["a", "b", "c"]。
例如,如果 s = "a{b,c}" ,第一个字符总是 'a' ,但第二个字符可以是 'b' 或 'c' 。原来的列表是 ["ab", "ac"] 。请你 按字典顺序 ,返回所有以这种方式形成的单词
字符串解码
优先队列
单调栈
二叉树
前序,中序以及后序遍历 迭代和递归方式
dfs与bfs
二叉排序树
贪心
最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组是数组中的一个连续部分。
无重叠区间
给定一个区间的集合 intervals ,其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。
注意 只在一点上接触的区间是 不重叠的。例如 [1, 2] 和 [2, 3] 是不重叠的。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
sort(intervals.begin(),intervals.end());
// 先通过排序 如果两个区间重叠,移除结束位置更靠后的区间
int sz = intervals.size();
int result{};
for(int i = 1;i<sz;i++) {
if(intervals[i][0]<intervals[i-1][1]) {
// 重叠 需要移除区间
// 比较哪个区间结束位置更靠前
result++;
intervals[i][1] = min(intervals[i-1][1],intervals[i][1]);
}
}
return result;
}
};
用最少的箭引爆气球
有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。
一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 x``start,x``end, 且满足 xstart ≤ x ≤ x``end,则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后,可以无限地前进。
给你一个数组 points ,返回引爆所有气球所必须射出的 最小 弓箭数
如果气球重叠了,重叠气球中右边边界的最小值 之前的区间一定需要一个弓箭1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int findMinArrowShots(vector<vector<int>>& points) {
sort(points.begin(),points.end());
int n = points.size();
int r{1};
for(int i =1;i<n;i++) {
if(points[i][0]>points[i-1][1]) {
r++;
}else{
points[i][1] = min(points[i-1][1],points[i][1]);
}
}
return r;
}
};
划分字母区间
字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
vector<int> partitionLabels(string s) {
// 同一个字母最多出现在一个分段中
// 记录字母最后位置
vector<int> cnts(26);
for (int i = 0; i < s.size(); i++) {
cnts[s[i] - 'a'] = i;
}
vector<int> r;
int start{};
int maxPos{};
for (int i = 0; i < s.size(); i++) {
maxPos = max(maxPos, cnts[s[i] - 'a']);
if (i == maxPos) {
// 到达最后位置
r.push_back(i - start + 1);
start = i+1;
}
}
return r;
}
};
合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
sort(intervals.begin(), intervals.end());
int n = intervals.size();
vector<vector<int>> r;
r.push_back(intervals[0]);
for (int i = 1; i < n; i++) {
if (intervals[i][0] <= r.back()[1]) {
// 进行合并
// 修改区间结束位置
r.back()[1] = max(intervals[i][1], r.back()[1]);
} else {
r.push_back(intervals[i]);
}
}
return r;
}
};
单调递增的数字
当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。
给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int monotoneIncreasingDigits(int n) {
string ns = to_string(n);
int sz = ns.size();
int flag{sz};
for (int i = sz - 2; i >= 0; i--) {
if (ns[i] > ns[i + 1]) {
// 不符合单增 当前位-1
ns[i] -= 1;
flag = i + 1;
}
}
for (int i = flag; i < sz; i++) {
ns[i] = '9';
}
return stoi(ns);
}
};
买卖股票
回溯
回溯法,一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
回溯模板:
- 回溯函数模板返回值以及参数
在回溯算法中,我的习惯是函数起名字为backtracking,这个起名大家随意。
回溯算法中函数返回值一般为void。再来看一下参数,因为回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来,所以一般是先写逻辑,然后需要什么参数,就填什么参数
- 回溯函数终止条件
什么时候达到了终止条件,树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。 - 回溯搜索的遍历过程
1 | for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) { |
组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案
在集合[1,2,3,4]取1之后,下一层递归,就要在[2,3,4]中取数了,那么下一层递归如何知道从[2,3,4]中取数呢,靠的就是startIndex。所以需要startIndex来记录下一层递归,搜索的起始位置。
如果for循环选择的起始位置之后的元素个数已经不足需要的元素个数了,那么就没有必要搜索了1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(int n, int k, int startIndex) {
if (path.size() == k) {
result.push_back(path);
return;
}
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { // 优化的地方
path.push_back(i); // 处理节点
backtracking(n, k, i + 1);
path.pop_back(); // 回溯,撤销处理的节点
}
}
public:
vector<vector<int>> combine(int n, int k) {
backtracking(n, k, 1);
return result;
}
};
组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。 对于给定的输入,保证和为 target 的不同组合数少于 150 个
进行剪枝,包括深度,和如果大于targetSum返回. 广度,和必须要与targetSum.
在求和问题中,排序之后加剪枝是常见的套路1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class Solution {
public:
void backtrace(vector<int>& candidates, int targetSum,
vector<vector<int>>& result, vector<int>& path, int startIdx,
int sumVal) {
// 截止条件
if (sumVal > targetSum) {
return;
}
if (sumVal == targetSum) {
result.push_back(path);
return;
}
for (int i = startIdx;
// 求和 排序之后剪枝
i < candidates.size() && sumVal + candidates[i] <= targetSum;
i++) {
path.push_back(candidates[i]);
// 可重复 所以递归下次索引还是i
backtrace(candidates, targetSum, result, path, i,
sumVal + candidates[i]);
path.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
sort(candidates.begin(), candidates.end());
// 可重复
vector<vector<int>> result;
vector<int> path;
backtrace(candidates, target, result, path, 0, 0);
return result;
}
};
组合总和II
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用一次。
说明: 所有数字(包括目标数)都是正整数。解集不能包含重复的组合1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution {
public:
void backtrace(vector<int>& candidates, int target,
vector<int>& path, vector<vector<int>>& result, int sumVal,int idx,vector<bool>& isUsed) {
// 截止条件
if (sumVal > target) {
return;
}
if(sumVal == target) {
result.push_back(path);
return;
}
for(int i = idx;i<candidates.size() && candidates[i]+sumVal<=target;i++) {
if(i>0 && candidates[i] == candidates[i-1] && isUsed[i-1] == false) {
// 表明同一树层使用过
continue;
}
isUsed[i] = true;
path.push_back(candidates[i]);
backtrace(candidates,target,path,result,sumVal+candidates[i],i+1,isUsed);
path.pop_back();
isUsed[i] = false;
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
// 不重复
vector<int> path;
vector<vector<int>> result;
sort(candidates.begin(), candidates.end());
vector<bool> isUsed(candidates.size());
backtrace(candidates, target, path, result,0,0,isUsed);
return result;
}
};
或者通过i>startIndex && candidate[i] == candidate[i-1]进行去重. 核心是同一树层去重1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution {
public:
void backtrace(vector<int>& candidates, int target,
vector<int>& path, vector<vector<int>>& result, int sumVal,int idx) {
// 截止条件
if (sumVal > target) {
return;
}
if(sumVal == target) {
result.push_back(path);
return;
}
for(int i = idx;i<candidates.size() && candidates[i]+sumVal<=target;i++) {
if(i>idx && candidates[i] == candidates[i-1] ) {
// 表明同一树层使用过
continue;
}
isUsed[i] = true;
path.push_back(candidates[i]);
backtrace(candidates,target,path,result,sumVal+candidates[i],i+1);
path.pop_back();
isUsed[i] = false;
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
// 不重复
vector<int> path;
vector<vector<int>> result;
sort(candidates.begin(), candidates.end());
vector<bool> isUsed(candidates.size());
backtrace(candidates, target, path, result,0,0);
return result;
}
};
组合总和III
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
- 所有数字都是正整数。
- 解集不能包含重复的组合。
1 | class Solution { |
已选元素总和如果已经大于n(图中数值为4)了,那么往后遍历就没有意义了,直接剪掉.for循环的范围也可以剪枝,i <= 9 - (k - path.size()) + 1。
分割
分割回文串
给你一个字符串 s,请你将 s 分割成一些 子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37class Solution {
public:
bool isPalin(string&s,int i,int j) {
int l = i,r=j;
while(l<r) {
if(s[l]!=s[r]) {
return false;
}
l++;
r--;
}
return true;
}
void backtrace(string& s,vector<string>& path,vector<vector<string>>& result,int startPos) {
// 截止条件
if(startPos == s.size()) {
result.push_back(path);
return;
}
for(int i = startPos;i<s.size();++i) {
// 判断子串回文
// 或者动规求dp[i][j]是否回文
bool isValid = isPalin(s,st artPos,i);
if(isValid) {
path.push_back(s.substr(startPos,i-startPos+1));
backtrace(s,path,result,i+1);
path.pop_back();
}
}
}
vector<vector<string>> partition(string s) {
vector<vector<string>> result;
vector<string> path;
backtrace(s,path,result,0);
return result;
}
};
在计算回文子串的时候可以使用dp进行计算优化1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44class Solution {
private:
vector<vector<string>> result;
vector<string> path; // 放已经回文的子串
vector<vector<bool>> isPalindrome; // 放事先计算好的是否回文子串的结果
void backtracking (const string& s, int startIndex) {
// 如果起始位置已经大于s的大小,说明已经找到了一组分割方案了
if (startIndex >= s.size()) {
result.push_back(path);
return;
}
for (int i = startIndex; i < s.size(); i++) {
if (isPalindrome[startIndex][i]) { // 是回文子串
// 获取[startIndex,i]在s中的子串
string str = s.substr(startIndex, i - startIndex + 1);
path.push_back(str);
} else { // 不是回文,跳过
continue;
}
backtracking(s, i + 1); // 寻找i+1为起始位置的子串
path.pop_back(); // 回溯过程,弹出本次已经添加的子串
}
}
void computePalindrome(const string& s) {
// isPalindrome[i][j] 代表 s[i:j](双边包括)是否是回文字串
isPalindrome.resize(s.size(), vector<bool>(s.size(), false)); // 根据字符串s, 刷新布尔矩阵的大小
for (int i = s.size() - 1; i >= 0; i--) {
// 需要倒序计算, 保证在i行时, i+1行已经计算好了
for (int j = i; j < s.size(); j++) {
if (j == i) {isPalindrome[i][j] = true;}
else if (j - i == 1) {isPalindrome[i][j] = (s[i] == s[j]);}
else {isPalindrome[i][j] = (s[i] == s[j] && isPalindrome[i+1][j-1]);}
}
}
}
public:
vector<vector<string>> partition(string s) {
result.clear();
path.clear();
computePalindrome(s);
backtracking(s, 0);
return result;
}
};
复原IP地址
有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
- 例如:
"0.1.2.201"和"192.168.1.1"是 有效 IP 地址,但是"0.011.255.245"、"192.168.1.312"和"192.168@1.1"是 无效 IP 地址。
给定一个只包含数字的字符串 s ,用以表示一个 IP 地址,返回所有可能的有效 IP 地址,这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案
startIndex一定是需要的,因为不能重复分割,记录下一层递归分割的起始位置。还需要一个变量pointNum,记录添加逗点的数量。本题明确要求只会分成4段,所以不能用切割线切到最后作为终止条件,而是分割的段数作为终止条件。pointNum表示逗点数量,pointNum为3说明字符串分成了4段了。然后验证一下第四段是否合法,如果合法就加入到结果集里.在for (int i = startIndex; i < s.size(); i++)循环中 [startIndex, i] 这个区间就是截取的子串,需要判断这个子串是否合法。
如果合法就在字符串后面加上符号.表示已经分割。
递归调用时,下一层递归的startIndex要从i+2开始(因为需要在字符串中加入了分隔符.),同时记录分割符的数量pointNum 要 +1。
回溯的时候,就将刚刚加入的分隔符. 删掉就可以了,pointNum也要-1。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56class Solution {
public:
bool isValidIp(string& s, int startPos, int endPos) {
// [startPos,endPos]
int len = endPos - startPos + 1;
if (len > 3 || len == 0) {
return false;
}
if (len > 1 && s[startPos] == '0') {
return false;
}
int ipNum{};
for (int i = startPos; i <= endPos; i++) {
ipNum = ipNum * 10 + (s[i] - '0');
if (ipNum > 255) {
return false;
}
}
if (ipNum >= 0 && ipNum <= 255) {
return true;
}
return false;
}
// 切割 回溯
void backtrace(string& s, vector<string>& result, int startPos,
int pointNum) {
// 结束条件
if (pointNum == 3) {
if (isValidIp(s, startPos, s.size() - 1)) {
result.push_back(s);
}
return;
}
for (int i = startPos; i < s.size(); i++) {
// 添加.分割
if (isValidIp(s, startPos, i)) {
// s[startPos,i]满足条件,在i之后添加分割
s.insert(s.begin() + i + 1, '.');
backtrace(s, result, i + 2, pointNum + 1);
s.erase(i + 1, 1);
} else {
// 不合法 直接结束
break;
}
}
}
vector<string> restoreIpAddresses(string s) {
vector<string> result;
if (s.size() < 4 || s.size() > 12) {
return {};
}
backtrace(s, result, 0, 0);
return result;
}
};
子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
如果把 子集问题、组合问题、分割问题都抽象为一棵树的话,那么组合问题和分割问题都是收集树的叶子节点,而子集问题是找树的所有节点!
其实子集也是一种组合问题,因为它的集合是无序的,子集{1,2} 和 子集{2,1}是一样的。
那么既然是无序,取过的元素不会重复取,写回溯算法的时候,for就要从startIndex开始,而不是从0开始!1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
void backtrace(vector<int>& nums, int startIdx, vector<vector<int>>& result,
vector<int>& path) {
// 结束条件
// 子集问题 需要收集这个回溯多叉树的每个节点
result.push_back(path);
for(int i = startIdx;i<nums.size();i++) {
path.push_back(nums[i]);
backtrace(nums,i+1,result,path);
path.pop_back();
}
}
vector<vector<int>> subsets(vector<int>& nums) {
vector<vector<int>> result;
vector<int> path;
backtrace(nums,0,result,path);
return result;
}
};
子集II
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的 子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
void backtrace(vector<int>& nums,int startIndex,vector<int>& path,vector<vector<int>>& result) {
// 结束条件
result.push_back(path);
for(int i = startIndex;i<nums.size();i++) {
if(i>startIndex && nums[i] == nums[i-1]) {
// 同一层使用过了
continue;
}
path.push_back(nums[i]);
backtrace(nums,i+1,path,result);
path.pop_back();
}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
sort(nums.begin(),nums.end());
vector<int> path;
vector<vector<int>> result;
backtrace(nums,0,path,result);
return result;
}
};
非递减子序列
给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。数组中可能含有重复元素,如出现两个整数相等,也可以视作递增序列的一种特殊情况。
本题求自增子序列,是不能对原数组进行排序的,排完序的数组都是自增子序列了。所以不能使用之前的去重逻辑. 同一父节点下的同层上使用过的元素就不能再使用了1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
// 子集问题
void backtrace(vector<int>& nums, vector<int>& path,
vector<vector<int>>& result, int startPos ) {
// 结束条件
if (path.size() >= 2) {
result.push_back(path);
}
vector<int> used(201);
for (int i = startPos; i < nums.size(); i++) {
if (used[nums[i]+100]) {
continue;
}
if (path.empty() || nums[i] >= path.back()) {
path.push_back(nums[i]);
// used.insert(nums[i]);
used[nums[i]+100] = true;
backtrace(nums, path, result, i + 1);
path.pop_back();
}
}
}
vector<vector<int>> findSubsequences(vector<int>& nums) {
vector<vector<int>> result;
vector<int> path;
vector<bool> used(nums.size());
backtrace(nums, path,result, 0);
return result;
}
};
排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案
排列是有序的,也就是说 [1,2] 和 [2,1] 是两个集合,这和之前分析的子集以及组合所不同的地方
used数组就是记录此时path里都有哪些元素使用了,一个排列里一个元素只能使用一次
排列问题的不同:
- 每层都是从0开始搜索而不是startIndex
- 需要used数组记录path里都放了哪些元素了
1 | class Solution { |
全排列II
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34class Solution {
public:
void backtrace(vector<int>& nums,vector<int>& path,vector<vector<int>>& result,vector<bool>& isUsed) {
if(path.size() == nums.size()) {
result.push_back(path);
return;
}
for(int i=0;i<nums.size();i++) {
// used[i - 1] == true,说明同一树枝nums[i - 1]使用过
// used[i - 1] == false,说明同一树层nums[i - 1]使用过
// 如果同一树层nums[i - 1]使用过则直接跳过
if(i>0 &&nums[i] == nums[i-1] && isUsed[i-1]==false) {
continue;
}
// 不能添加同一个元素到path
if(isUsed[i]) {
continue;
}
path.push_back(nums[i]);
isUsed[i] = true;
backtrace(nums,path,result,isUsed);
path.pop_back();
isUsed[i] = false;
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
vector<vector<int>> result;
vector<int> path;
sort(nums.begin(),nums.end());
vector<bool> isUsed(nums.size());
backtrace(nums,path,result,isUsed);
return result;
}
};
棋盘
N皇后
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47class Solution {
private:
vector<vector<string>> result;
// n 为输入的棋盘大小
// row 是当前递归到棋盘的第几行了
void backtracking(int n, int row, vector<string>& chessboard) {
if (row == n) {
result.push_back(chessboard);
return;
}
for (int col = 0; col < n; col++) {
if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
chessboard[row][col] = 'Q'; // 放置皇后
backtracking(n, row + 1, chessboard);
chessboard[row][col] = '.'; // 回溯,撤销皇后
}
}
}
bool isValid(int row, int col, vector<string>& chessboard, int n) {
// 检查列
for (int i = 0; i < row; i++) { // 这是一个剪枝
if (chessboard[i][col] == 'Q') {
return false;
}
}
// 检查 45度角是否有皇后
for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
// 检查 135度角是否有皇后
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
return true;
}
public:
vector<vector<string>> solveNQueens(int n) {
result.clear();
std::vector<std::string> chessboard(n, std::string(n, '.'));
backtracking(n, 0, chessboard);
return result;
}
};
解数独
1 | class Solution { |
数学问题
动态规划
动态规划的核心在于定义状态。你需要一个能表示子问题最优解的状态,并且这个状态要能通过之前的状态推导出来。
线性动态规划
线性动态规划:具有「线性」阶段划分的动态规划方法统称为线性动态规划(简称为「线性 DP」)
如果状态包含多个维度,但是每个维度上都是线性划分的阶段,也属于线性 DP。比如背包问题、区间 DP、数位 DP 等都属于线性 DP。
线性 DP 问题的划分方法有多种方式。
- 如果按照「状态的维度数」进行分类,我们可以将线性 DP 问题分为:一维线性 DP 问题、二维线性 DP 问题,以及多维线性 DP 问题。
- 如果按照「问题的输入格式」进行分类,我们可以将线性 DP 问题分为:单串线性 DP 问题、双串线性 DP 问题、矩阵线性 DP 问题,以及无串线性 DP 问题。
单串线性DP

这 3 种状态的定义区别在于相差一个元素 nums[i]。
- 第 1 种状态:子数组的长度为 i+1,子数组长度不可为空;
- 第 2 种状态、第 3种状态:这两种状态描述是相同的。子数组的长度为 i,子数组长度可为空。在 i=0时,方便用于表示空数组(以数组中前 00 个元素为子数组)
最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n = nums.size();
vector<int> dp(n, 1);
int r{1};
// dp[i]以nums[i]结尾的子序列的最长递增长度
// if(nums[i]>nums[j])
// dp[i] = max(dp[i],dp[j]+1)
for (int i = 1; i < n; ++i) {
for (int j = 0; j < i; j++) {
if (nums[i] > nums[j]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
r = max(r,dp[i]);
}
return r;
}
};
最大子数组之和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组是数组中的一个连续部分。
最长的斐波那契子序列的长度
有一些单串线性 DP 问题在定义状态时需要考虑两个结束位置,只考虑一个结束位置的无法清楚描述问题。这时候我们就需要需要增加一个结束位置维度来定义状态
如果序列 x1, x2, ..., xn 满足下列条件,就说它是 斐波那契式 的:
n >= 3- 对于所有
i + 2 <= n,都有xi + xi+1 == xi+2
给定一个 严格递增 的正整数数组形成序列 arr ,找到 arr 中最长的斐波那契式的子序列的长度。如果不存在,返回 0 。
子序列 是通过从另一个序列 arr 中删除任意数量的元素(包括删除 0 个元素)得到的,同时不改变剩余元素顺序。例如,[3, 5, 8] 是 [3, 4, 5, 6, 7, 8] 的子序列。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29class Solution {
public:
int lenLongestFibSubseq(vector<int>& arr) {
int n = arr.size();
if (n < 3) {
return 0;
}
vector<vector<int>> dp(
n, vector<int>(
n, 2)); // dp[i][j]以arr[i],arr[j]结尾的最长斐波那契式子序列
// 初始化
unordered_map<int, int> umap;
for (int i = 0; i < n; ++i) {
umap.insert({arr[i], i});
}
int r{};
for (int i = 0; i < n; ++i) {
for (int j = i + 1; j < n; j++) {
// 以 arr[j] arr[i]结尾的最长斐波那契式子序列
if (umap.count(arr[i] + arr[j])) {
int k = umap[arr[i] + arr[j]];
dp[j][k] = max(dp[i][j] + 1, dp[j][k]);
r = max(r, dp[j][k]);
}
}
}
return r;
}
};
双串线性DP

这 3 种状态的定义区别在于相差一个元素 nums1[i] 或 nums2[j]
- 第 1 种状态:子数组的长度为 i+1 或 j+1,子数组长度不可为空
- 第 2 种状态、第 3 种状态:子数组的长度为 i或 j,子数组长度可为空。i=0或 j=0时,方便用于表示空数组(以数组中前 00 个元素为子数组)。
最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"是"abcde"的子序列,但"aec"不是"abcde"的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
int n1 = text1.size();
int n2 = text2.size();
vector<vector<int>> dp(
n1 + 1,
vector<int>(n2 + 1)); // dp[i][j] 前i,j个子串的最长公共子序列
for (int i = 1; i <= n1; i++) {
for (int j = 1; j <= n2; j++) {
if (text1[i - 1] == text2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}else{
dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
}
}
}
return dp[n1][n2];
}
};
最长重复子数组
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2) {
int n1 = nums1.size();
int n2 = nums2.size();
// 以nums1[i-1]和nums[j-1]结尾的子串的公共最长子数组长度
vector<vector<int>> dp(n1 + 1, vector<int>(n2 + 1));
int r{};
for(int i = 1;i<=n1;i++) {
for(int j = 1;j<=n2;j++) {
if(nums1[i-1] == nums2[j-1]) {
dp[i][j] = dp[i-1][j-1]+1;
}else{
dp[i][j] = 0;
}
r = max(r,dp[i][j]);
}
}
return r;
}
};
编辑距离
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
1 | class Solution { |
矩形线性DP
矩阵线性 DP 问题:问题的输入为二维矩阵的线性 DP 问题。状态一般可定义为 dp[i][j],表示为:从「位置 (0,0)(0,0)」到达「位置 (i,j)」的相关解
最小路径和
给定一个包含非负整数的 *m* x *n* 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
// 到达(m,n)位置的路径最小数字
vector<vector<int>> dp(m,vector<int>(n));
dp[0][0] = grid[0][0];
for (int i = 1; i < m; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
for (int j = 1; j < n; j++) {
dp[0][j] = dp[0][j - 1] + grid[0][j];
}
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
dp[i][j] =
min(dp[i - 1][j] + grid[i][j], dp[i][j - 1] + grid[i][j]);
}
}
return dp[m-1][n-1];
}
};
最大正方形
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
// dp[i][j]表示以matrix[i][j]右下角的只包含1最大正方形边长
// dp[i][j] = dp[i-1][j-1]+1 if matrix[i][j] == 1 &&
// matrix[i][j-dp[i-1][j-1]]->matrix[i][j] = 1 &&
// matrix[i-dp[i-1][j-1]][j]->matrix[i-dp[i-1][j-1]][j] = 1
vector<vector<int>> dp(m, vector<int>(n));
// 初始化
int maxLen{0};
for (int i = 0; i < m; i++) {
dp[i][0] = (matrix[i][0] == '1');
maxLen = max(maxLen, dp[i][0]);
}
for (int j = 0; j < n; j++) {
dp[0][j] = (matrix[0][j] == '1');
maxLen = max(maxLen, dp[0][j]);
}
// 状态转移
for (int i = 1; i < m; ++i) {
for (int j = 1; j < n; ++j) {
// 如果满足条件
if (matrix[i][j] == '1') {
dp[i][j] =
min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) +
1;
maxLen = max(maxLen, dp[i][j]);
}
}
}
return maxLen * maxLen;
}
};
无串线性DP
无串线性 DP 问题:问题的输入不是显式的数组或字符串,但依然可分解为若干子问题的线性 DP 问题。
整数拆分
给定一个正整数 nn,将其拆分为 k(k≥2)个正整数的和,并使这些整数的乘积最大化。1
2
3
4
5
6
7
8
9
10
11
12
13
14class Solution {
public:
int integerBreak(int n) {
vector<int> dp(n + 1); // dp[i]表示整数i的拆分乘积最大值
// dp[i] = max(k*dp[i-k])
dp[2] = 1;
for (int i = 3; i <= n; i++) {
for (int j = 1; j < i; j++) {
dp[i] = max(dp[i], max(j * dp[i - j],j*(i-j)));
}
}
return dp[n];
}
};
两个键的键盘
最初记事本上只有一个字符 'A' 。你每次可以对这个记事本进行两种操作:
Copy All(复制全部):复制这个记事本中的所有字符(不允许仅复制部分字符)。Paste(粘贴):粘贴 上一次 复制的字符。
给你一个数字 n ,你需要使用最少的操作次数,在记事本上输出 恰好 n 个 'A' 。返回能够打印出 n 个 'A' 的最少操作次数1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20class Solution {
public:
int minSteps(int n) {
// dp[i]表示有i个A的最少操作
if (n == 1) {
return 0;
}
vector<int> dp(n + 1, INT_MAX);
dp[1] = 0;
for (int i = 2; i <= n; ++i) {
for (int j = 1; j * j <= i; j++) {
if (i % j == 0) {
dp[i] = min(dp[i], dp[j] + i / j);
dp[i] = min(dp[i], dp[i / j] + j);
}
}
}
return dp[n];
}
};
区间动态规划
区间动态规划:线性 DP 的一种,简称为「区间 DP」。以「区间长度」划分阶段,以两个坐标(区间的左、右端点)作为状态的维度。一个状态通常由被它包含且比它更小的区间状态转移而来。
区间 DP 的主要思想就是:先在小区间内得到最优解,再利用小区间的最优解合并,从而得到大区间的最优解,最终得到整个区间的最优解。
根据小区间向大区间转移情况的不同,常见的区间 DP 问题可以分为两种:
- 单个区间从中间向两侧更大区间转移的区间 DP 问题。比如从区间 [i+1,j−1] 转移到更大区间 [i,j]。
- 多个(大于等于 2 个)小区间转移到大区间的区间 DP 问题。比如从区间 [i,k]和区间 [k,j] 转移到区间 [i,j]

多个(大于等于 22 个)小区间转移到大区间的区间 DP 问题。比如从区间 [i,k] 和区间 [k,j] 转移到区间 [i,j]

回文子串
给定一个字符串 s ,请计算这个字符串中有多少个回文子字符串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
int countSubstrings(string s) {
int sz = s.size();
vector<vector<bool>> dp(sz, vector<bool>(sz));
// dp[i][j]表示以s[i]开始 以s[j]截止的子字符串是否为回文
int res{};
for (int i = sz-1;i>=0;i--) {
for (int j = i; j < sz; j++) {
if (i == j) {
dp[i][j] = true;
} else if (i == j - 1) {
dp[i][j] = s[i] == s[j];
} else {
dp[i][j] = (s[i] == s[j]) && dp[i + 1][j - 1];
}
if (dp[i][j]) {
res++;
}
}
}
return res;
}
};
最长回文子串
给你一个字符串 s,找到 s 中最长的 回文 子串。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31class Solution {
public:
string longestPalindrome(string s) {
// dp[i][j] 表示子字符串s[i]-s[j]是否回文
int sz = s.size();
vector<vector<bool>> dp(sz, vector<bool>(sz));
int max_l{};
int res{};
for (int i = sz - 1; i >= 0; i--) {
for (int j = i; j < sz; j++) {
if (i == j) {
dp[i][j] = true;
} else if (i == j - 1) {
if (s[i] == s[j]) {
dp[i][j] = true;
}
} else {
dp[i][j] = (s[i] == s[j]) && dp[i + 1][j - 1];
}
if (dp[i][j]) {
int len = j - i + 1;
if (len > res) {
res = len;
max_l = i;
}
}
}
}
return s.substr(max_l, res);
}
};
最长回文子序列
描述:给定一个字符串 s
要求:找出其中最长的回文子序列,并返回该序列的长度1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22class Solution {
public:
int longestPalindromeSubseq(string s) {
int n = s.size();
// dp[i][j]表示以[i,j]子串的最长回文子序列长度
vector<vector<int>> dp(n, vector<int>(n));
for (int i = n - 1; i >= 0; i--) {
for (int j = i; j < n; j++) {
if (i == j) {
dp[i][j] = 1;
} else {
if (s[i] == s[j]) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
}
return dp[0][n - 1];
}
};
戳气球
有 n 个气球,编号为0 到 n - 1,每个气球上都标有一个数字,这些数字存在数组 nums 中。
现在要求你戳破所有的气球。戳破第 i 个气球,你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。 这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界,那么就当它是一个数字为 1 的气球。求所能获得硬币的最大数量。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21class Solution {
public:
int maxCoins(vector<int>& nums) {
int n = nums.size();
nums.insert(nums.begin(), 1);
nums.push_back(1);
vector<vector<int>> dp(n + 2, vector<int>(n + 2));
// dp[i][j]表示在区间[i,j]戳破其中气球(不包括i,j)]得到的最大硬币
// k是这个区间最后一个戳破的气球
// dp[i][j] = max(dp[i][k] + dp[k][j]) j>=k>=i
for (int i = n - 1; i >= 0; i--) {
for (int j = i + 2; j <= n + 1; ++j) {
for (int k = i + 1; k < j; k++) {
dp[i][j] = max(dp[i][j], dp[i][k] + dp[k][j] +
nums[k] * nums[i] * nums[j]);
}
}
}
return dp[0][n + 1];
}
};
切棍子的最小成本
有一根长度为 n 个单位的木棍,棍上从 0 到 n 标记了若干位置。给你一个整数数组 cuts ,其中 cuts[i] 表示你需要将棍子切开的位置。
你可以按顺序完成切割,也可以根据需要更改切割的顺序。
每次切割的成本都是当前要切割的棍子的长度,切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍(这两根木棍的长度和就是切割前木棍的长度)。请参阅第一个示例以获得更直观的解释。返回切棍子的 最小总成本 。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24class Solution {
public:
int minCost(int n, vector<int>& cuts) {
cuts.push_back(0);
cuts.push_back(n);
sort(cuts.begin(), cuts.end());
int m = cuts.size();
// dp[i][j] 在位置i,j中(不包括i,j)进行切割得到的最小总成本
vector<vector<int>> dp(m, vector<int>(m, INT_MAX));
for (int i = 0; i < m - 1; i++) {
dp[i][i + 1] = 0;
}
for (int i = m - 3; i >= 0; i--) {
for (int j = i + 2; j < m; j++) {
for (int k = i + 1; k < j; k++) {
// 在(i,j)之间
dp[i][j] =
min(dp[i][j], dp[i][k] + dp[k][j] + cuts[j] - cuts[i]);
}
}
}
return dp[0][m - 1];
}
};
树形动态规划
树形动态规划:简称为「树形 DP」,是一种在树形结构上进行推导的动态规划方法。树形 DP 的求解过程一般以节点从深到浅(子树从小到大)的顺序作为动态规划的「阶段」。
在树形 DP 中,第 1 维通常是节点编号,代表以该节点为根的子树。
二叉树的最大路径和
描述:给定一个二叉树的根节点 root。要求:返回其最大路径和。
二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int maxVal{INT_MIN};
int maxGain(TreeNode* node) {
if (!node) {
return 0;
}
int left = max(maxGain(node->left), 0);
int right = max(maxGain(node->right), 0);
maxVal = max(maxVal,left + right + node->val);
return max(left,right)+node->val;
}
int maxPathSum(TreeNode* root) {
maxGain(root);
return maxVal;
}
};
相邻字符的不同最长路径
1 | class Solution { |
数位动态规划
数位动态规划:简称为「数位 DP」,是一种与数位相关的一类计数类动态规划问题,即在数位上进行动态规划。这里的数位指的是个位、十位、百位、千位等
数位 DP 一般用于求解给定区间[left,right] 中,满足特定条件的数值个数,或者用于求解满足特定条件的第 kk 小数。
数位 DP 通常有以下几个特征:
- 题目会提供一个查询区间(有时也会只提供区间上界)来作为统计限制。
- 题目中给定区间往往很大(比如 109109),无法采用朴素的方法求解。
- 题目中给定的给定的限定条件往往与数位有关。
- 要求统计满足特定条件的数值个数,或者用于求解满足特定条件的第 k 小数
将区间上的数字按照数位进行拆分,然后逐位确定每一个数位上的可行方案,从而计算出区间内的可行方案个数。
数位 DP 的基本思想:将区间数字拆分为数位,然后逐位进行确定。数位 DP 可以通过「记忆化搜索」的方式实现,也可以通过「迭代递推」的方式实现。因为数位 DP 中需要考虑的参数很多,使用「记忆化搜索」的方式更加方便传入参数,所以这里采用「记忆化搜索」的方式来实现。
数字1的个数
给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26class Solution {
public:
int dfs(string& ns, int pos, int cnt, bool isLimit,vector<vector<int>>& memo) {
if (pos == ns.size()) {
return cnt;
}
if(!isLimit && memo[pos][cnt]>=0) {
return memo[pos][cnt];
}
int ans = 0;
int up = isLimit ? (ns[pos] - '0') : 9;
for (int i = 0; i <= up; i++) {
ans += dfs(ns,pos + 1, cnt + (i == 1), isLimit && (i == up),memo);
}
if(!isLimit) {
memo[pos][cnt] = ans;
}
return ans;
}
int countDigitOne(int n) {
string ns = to_string(n);
int t = ns.size();
vector<vector<int>> memo(t,vector<int>(t,-1)); // 记忆化 避免超内存
return dfs(ns,0, 0, true,memo);
}
};
至少一位重复数字
给定正整数 n,返回在 [1, n] 范围内具有 至少 1 位 重复数字的正整数的个数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37class Solution {
public:
int dfs(string& ns, int pos, int state, bool isLimit, bool isNum,vector<vector<int>>& memo) {
if (ns.size() == pos) {
return isNum;
}
int ans = 0;
if(!isLimit&& isNum && memo[pos][state]>=0) {
return memo[pos][state];
}
if (!isNum) {
// 如果之前位没有填数字
// 可以跳过
ans = dfs(ns, pos + 1, state, false, false,memo);
}
int minX = isNum ? 0 : 1;
int up = isLimit ? ns[pos] - '0' : 9;
for (int i = minX; i <= up; i++) {
if (((state >> i) & 1 )== 0) {
// 对应位没有选择
ans += dfs(ns, pos + 1, state | (1 << i), isLimit && (i == up),
true,memo);
}
}
if(!isLimit&& isNum) {
memo[pos][state] = ans;
}
return ans;
}
int numDupDigitsAtMostN(int n) {
string ns = to_string(n);
int sz = ns.size();
vector<vector<int>> memo(sz,vector<int>(1<<10,-1));
// 求解不重复数字然后 n-ans
return n-dfs(ns, 0, 0, true, false,memo);
}
};
背包问题
背包有多种类型,包括01背包,完全背包,多重背包等等. 这里主要讲01背包和完全背包.
背包问题:背包问题是线性 DP 问题中一类经典而又特殊的模型。背包问题可以描述为:给定一组物品,每种物品都有自己的重量、价格以及数量。再给定一个最多能装重量为 WW 的背包。现在选择将一些物品放入背包中,请问在总重量不超过背包载重上限的情况下,能装入背包的最大价值总和是多少?
01背包
0-1 背包问题:有 n件物品和有一个最多能装重量为 W的背包。第 i件物品的重量为 weight[i],价值为 value[i],每件物品有且只有1 件。请问在总重量不超过背包载重上限的情况下,能装入背包的最大价值是多少?8.5 背包问题(一) | 算法通关手册(LeetCode)
0-1 背包问题的特点:每种物品有且仅有 1 件,可以选择不放入背包,也可以选择放入背包。其第一维代表「当前正在考虑的物品」,第二维表示「当前背包的载重上限」,二维数组值表示「可以获得的最大价值」
想象一下01背包的dp数组,dp[i][j]表示前 i件物品放入一个最多能装重量为 w的背包中,可以获得的最大价值. 一个二维表格,行为物品,列为容量. 每个值由上一行的同一列以及另一列求得.
分割等和子集
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
只要找到集合里能够出现 sum / 2 的子集总和,就算是可以分割成两个相同元素和子集了
目标和
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
//
int sumVal = accumulate(nums.begin(), nums.end(), 0);
// 正数 + abs(负数) = sumVal
// 正数 +负数 = target
// 正数 = (sumVal+target)/2;
int n = nums.size();
if ((sumVal + target) % 2) {
return 0;
}
int targetVal = (sumVal + target) / 2;
if (targetVal<0 || targetVal > sumVal) {
return 0;
}
vector<int> dp(targetVal + 1); // dp[i]和为i的数目 01背包
// 初始化
dp[0] = 1;
for (int i = 0; i < n; ++i) {
for (int j = targetVal; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[targetVal];
}
};
最后一块石头的重量
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 01
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
int sumVal = accumulate(stones.begin(), stones.end(), 0);
// 尽可能求得sumVal/2
int target = sumVal / 2;
vector<int> dp(target + 1); // dp[i]表示和为i的最大值
for (int i = 0; i < stones.size(); i++) {
for (int j = target; j >= stones[i]; j--) {
// dp[j]是上一轮的值
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sumVal - dp[target] - dp[target];
}
};
完全背包
完全背包问题:有 n种物品和一个最多能装重量为 W 的背包,第 i 种物品的重量为 weight[i],价值为 value[i],每种物品数量没有限制。请问在总重量不超过背包载重上限的情况下,能装入背包的最大价值是多少?
完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int numSquares(int n) {
// dp[i]表示和为i的完全平方数的最少数量
vector<int> dp(n + 1,INT_MAX);
// dp[i] = dp[j] + 1; if(j+(i-j)^2 == i)
dp[0] = 0;
dp[1] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = 1; j * j <= i; j++) {
dp[i] = min(dp[i],dp[i - j * j] + 1);
}
}
return dp[n];
}
};
零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。你可以认为每种硬币的数量是无限的。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount + 1, INT_MAX); // dp[i]凑成金额i所需的最少硬币数
dp[0] = 0;
// dp[j] = min(dp[j-coins[i]] + coins[i]);
// 完全背包
for (int i = 0; i < coins.size(); ++i) {
for (int j = coins[i]; j <= amount; j++) {
if (dp[j - coins[i]] == INT_MAX) {
continue;
}
dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
}
}
return dp[amount] == INT_MAX ? -1 : dp[amount];
}
};
零钱兑换III
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带符号整数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18class Solution {
public:
int change(int amount, vector<int>& coins) {
// 方案数
// 组合 完全背包
int n = coins.size();
vector<int> dp(amount + 1); // 凑到金额i的方案数
dp[0] = 1;
for (int i = 0; i < n; ++i) {
for (int j = 1; j <= amount; j++) {
if (j >= coins[i] && dp[j]<=INT_MAX-dp[j-coins[i]]) {
dp[j] += dp[j - coins[i]];
}
}
}
return dp[amount];
}
};
组合总和IV
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int combinationSum4(vector<int>& nums, int target) {
// 排列数
vector<int> dp(target + 1); // dp[i]表示和为i的方案数 排列
dp[0] = 1;
for (int j = 1; j <=target ; j++) {
for (int i = 0; i < nums.size(); i++) {
if (j >= nums[i] && dp[j] <= INT_MAX - dp[j - nums[i]]) {
dp[j] += dp[j - nums[i]];
}
}
}
return dp[target];
}
};
背包变种问题
8.9 背包问题(五) | 算法通关手册(LeetCode)
求恰好装满背包的最大价值
0-1 背包问题求恰好装满背包的最大价值:有 n 种物品和一个最多能装重量为 W 的背包,第 ii* 种物品的重量为 weight[i],价值为 value[i,每件物品有且只有 1件。请问在恰好装满背包的情况下,能装入背包的最大价值总和是多少?
如果要求恰好装满背包,那么:
- 只有载重上限为 0 的背包,在不放入物品时,能够恰好装满背包(有合法解),此时背包所含物品的最大价值为 0,即 dp[0]=0。
- 其他载重上限下的背包,在放入物品的时,都不能恰好装满背包(都没有合法解),此时背包所含物品的最大价值属于未定义状态,值应为 −∞ .这样在进行状态转移时,我们可以通过判断 dp[w] 与 −∞ 的关系,来判断是否能恰好装满背包
求方案总数
背包问题求方案数:在给定背包重量 W,每件物品重量 weight[i],物品间相互关系(分组、依赖等)的背包问题中,请问在总重量不超过背包载重上限的情况下,或者在总重量不超过某一指定重量的情况下,一共有多少种方案?
将原有状态转移方程中的「求最大值」变为「求和」即可
- 如果使用二维状态定义,可定义状态 dp[i][j]为:前 i件物品放入一个最多能装重量为 w的背包中的方案总数。则状态转移方程为:dp[i][w]=dp[i−1][w]+dp[i][w−weight[i−1]]。
- 如果使用一维状态定义,可定义状态 dp[w] 表示为:将物品装入一个最多能装重量为 w 的背包中的方案总数。则状态转移方程为:dp[w]=dp[w]+dp[w−weight[i−1]]
如果背包载重上限为 0,则一共有 1 种方案(什么也不装),即 dp[0]=1
求最优方案数
背包问题求最优方案数:在给定背包重量 W,每件物品重量 weight[i]、物品价值 value[i],物品间相互关系(分组、依赖等)的背包问题中,请问在总重量不超过背包载重上限的情况下,使背包总价值最大的方案数是多少?
- 定义 dp[i][w]表示为:前 i种物品放入一个最多能装重量为 w 的背包中,可获得的最大价值。
定义 op[i][w]表示为:前 i种物品放入一个最多能装重量为 w的背包中,使背包总价值最大的方案数
- 如果 dp[i−1][w]<dp[i−1][w−weight[i−1]]+value[i−1],则说明选择第 i−1 件物品获得价值更高,此时方案数 op[i][w] 是在 op[i−1][w−weight[i−1]] 基础上添加了第 i−1 件物品,因此方案数不变,即:op[i][w]=op[i−1][w−weight[i−1]]
- 如果 dp[i−1][w]=dp[i−1][w−weight[i−1]]+value[i−1],则说明选择与不选择第 i−1件物品获得价格相等,此时方案数应为两者之和,即:op[i][w]=op[i−1][w]+op[i−1][w−weight[i−1]]
- 如果 dp[i−1][w]>dp[i−1][w−weight[i−1]]+value[i−1],则说明不选择第 i−1件物品获得价值更高,此时方案数等于之前方案数,即:op[i][w]=op[i−1][w]
- 初始条件:如果背包载重上限为 0,则一共有 1 种方案(什么也不装),即 dp[0]=1
- 最终结果:根据我们之前定义的状态, op[i][w]表示为:前 i 种物品放入一个最多能装重量为 w的背包中,使背包总价值最大的方案数。则最终结果为 op[size][W],其中 size为物品的种类数,W 为背包的载重上限
求具体方案
背包问题求具体方案:在给定背包重量 WW,每件物品重量 weight[i]weigh**t[i]、物品价值 value[i]value[i],物品间相互关系(分组、依赖等)的背包问题中,请问将哪些物品装入背包,可使这些物品的总重量不超过背包载重上限,且价值总和最大?

任务批处理负载均衡
一个云计算中心接收到了一系列需要连续处理的微任务。现在有 nn 个任务排成一队,每个任务都有一个已知的计算成本。为了高效利用服务器资源,系统需要将这 nn 个连续的任务划分成 mm 个“批次”进行处理。
划分的规则是:必须按照任务队列的顺序进行划分,不能打乱任务原有的先后次序。例如,第一个批次处理前 k1k1 个任务,第二个批次处理接下来的 k2k2 个任务,以此类推。
为了使服务器负载尽可能平稳,调控目标是:找到一种划分方案,使得这 mm 个批次各自的“总计算成本”(即批次内所有任务的成本之和)的标准差达到最小。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
using namespace std;
int main() {
int n, m;
cin >> n >> m; // 任务总数 批次
vector<int> nums(n);
for (int i = 0; i < n; i++) {
cin >> nums[i];
}
vector<long long> prefix_sum(1 + n);
for (int i = 0; i < n; i++) {
prefix_sum[i + 1] = prefix_sum[i] + nums[i];
}
// 任务转化为最小化批次的和的最小平方和
// 前i个任务分j个批次的最小平方和
vector<vector<long long>> dp(n + 1, vector<long long>(m + 1, numeric_limits<long long>::max()));
vector<vector<int>> path(n + 1, vector<int>(m + 1,
0)); // 进行分批的结束位置
// dp[0][0] = 0;
for(int i = 0;i<=n;i++) {
dp[i][1] = prefix_sum[i]*prefix_sum[i];
}
//状态转移方程
for (int i = 1; i <= n; i++) {
for (int j = 2; j <= m; j++) {
// 从不同起点开始
for (int k = j - 1; k < i; k++) {
int r = dp[k][j - 1] + (prefix_sum[i] - prefix_sum[k]) *
(prefix_sum[i] - prefix_sum[k]);
if (r < dp[i][j]) {
dp[i][j] = r;
path[i][j] = k;
}
}
}
// 最终得到 前i个任务队列分j+1批的最小平方和
}
// 找到分界点
int cur = n;
vector<int> r;
for (int i = m; i >= 1; i--) {
int k = path[cur][i];
r.push_back(cur - k); // 长度
cur = k;
}
for (int i = r.size() - 1; i >= 0; i--) {
cout << r[i] << ((i == 0) ? '\n' : ' ');
}
return 0;
}
// 64 位输出请用 printf("%lld")
求字典序最小的方案
这里的「字典序最小」指的是序号为 0∼size−1的物品选择方案排列出来之后的字典序最小。
仍以「0-1 背包问题」求字典序最小的具体方案为例。
为了使「字典序最小」。可以先将物品的序号进行反转,从 0∼size−1变为 size−1∼0,然后在返回具体方案时,再根据 i=size−1 将序号变回来。
这是为了在选择物品时,尽可能的向后选择反转后序号大的物品(即原序号小的物品),从而保证原序号为 0∼size−1的物品选择方案排列出来之后的字典序最小。
打家劫舍
买卖股票最佳时机
子序列
字符串编辑
图论
数据结构
邻接矩阵
邻接表
邻接表 使用 数组 + 链表的方式来表示。 邻接表是从边的数量来表示图,有多少边 才会申请对应大小的链表。
深度优先
广度优先
单源最短路径
单源最短路径(Single Source Shortest Path):对于一个带权图 G=(V,E),其中每条边的权重是一个实数。另外,给定 vv 中的一个顶点,称之为源点。则源点到其他所有各个顶点之间的最短路径长度,称为单源最短路径。
单源最短路径问题的核心是找到从源点到其他各个顶点的路径,使得路径上边的权重之和最小。这个问题在许多实际应用中都非常重要,比如网络路由、地图导航、通信网络优化等。
常见的解决单源最短路径问题的算法包括:
- Dijkstra 算法:一种贪心算法,用于解决无负权边的情况。它逐步扩展当前已知最短路径的范围,选择当前距离起始节点最近的节点,并更新与该节点相邻的节点的距离。
- Bellman-Ford 算法:适用于有负权边的情况。它通过多次迭代来逐步逼近最短路径,每次迭代都尝试通过更新边的权重来缩短路径。
- SPFA 算法:优化的 Bellman-Ford 算法,它在每次迭代中不遍历所有的边,而是选择性地更新与当前节点相关的边,从而提高了算法的效率。
dijkstra及其堆优化
dijkstra三部曲:
- 第一步,选源点到哪个节点近且该节点未被访问过
- 第二步,该最近节点被标记访问过
- 第三步,更新非访问节点到源点的距离(即更新minDist数组)
Dijkstra 算法是一种用来解决单源最短路径问题的算法。这个算法适用于没有负权边的图。算法的核心思想是从源点出发,逐步找到到其他所有点的最短路径。它通过不断选择当前距离源点最近的节点,并更新与该节点相邻的节点的距离,最终得到所有节点的最短路径。
Dijkstra 算法使用贪心的策略。它每次选择当前未处理的节点中距离源点最近的节点,认为这个节点的最短路径已经确定。然后,它用这个节点的最短路径去更新其他相邻节点的距离。这个过程重复进行,直到所有节点的最短路径都被确定。
Dijkstra 算法的一个重要特点是它不能处理有负权边的图。因为负权边可能导致已经确定的最短路径被破坏。如果图中存在负权边,应该使用 Bellman-Ford 算法或 SPFA 算法。
- 初始化距离数组,将源节点 source的距离设为0,其他节点的距离设为无穷大。
- 维护一个访问数组 visited,记录节点是否已经被访问。
- 每次从未访问的节点中找到距离最小的节点,标记为已访问。
- 更新该节点的所有相邻节点的距离。
- 重复步骤 3∼4,直到所有节点都被访问。
- 最后返回所有节点中最大的距离值,如果存在无法到达的节点则返回 −1。
1 |
|
一般使用堆优化版适合稀疏图,1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
using namespace std;
// 小顶堆
class mycomparison {
public:
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs) {
return lhs.second > rhs.second;
}
};
// 定义一个结构体来表示带权重的边
struct Edge {
int to; // 邻接顶点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<list<Edge>> grid(n + 1);
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2,权值为 val
grid[p1].push_back(Edge(p2, val));
}
int start = 1; // 起点
int end = n; // 终点
// 存储从源点到每个节点的最短距离
std::vector<int> minDist(n + 1, INT_MAX);
// 记录顶点是否被访问过
std::vector<bool> visited(n + 1, false);
// 优先队列中存放 pair<节点,源点到该节点的权值>
priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pq;
// 初始化队列,源点到源点的距离为0,所以初始为0
pq.push(pair<int, int>(start, 0));
minDist[start] = 0; // 起始点到自身的距离为0
while (!pq.empty()) {
// 1. 第一步,选源点到哪个节点近且该节点未被访问过 (通过优先级队列来实现)
// <节点, 源点到该节点的距离>
pair<int, int> cur = pq.top(); pq.pop();
if (visited[cur.first]) continue;
// 2. 第二步,该最近节点被标记访问过
visited[cur.first] = true;
// 3. 第三步,更新非访问节点到源点的距离(即更新minDist数组)
for (Edge edge : grid[cur.first]) { // 遍历 cur指向的节点,cur指向的节点为 edge
// cur指向的节点edge.to,这条边的权值为 edge.val
if (!visited[edge.to] && minDist[cur.first] + edge.val < minDist[edge.to]) { // 更新minDist
minDist[edge.to] = minDist[cur.first] + edge.val;
pq.push(pair<int, int>(edge.to, minDist[edge.to]));
}
}
}
if (minDist[end] == INT_MAX) cout << -1 << endl; // 不能到达终点
else cout << minDist[end] << endl; // 到达终点最短路径
}
Bellman_ford算法以及队列优化
Bellman_ford算法的核心思想是对所有边进行松弛n-1次操作(n为节点数量),从而求得目标最短路1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
using namespace std;
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<vector<int>> grid;
// 将所有边保存起来
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2,权值为 val
grid.push_back({p1, p2, val});
}
int start = 1; // 起点
int end = n; // 终点
vector<int> minDist(n + 1 , INT_MAX);
minDist[start] = 0;
for (int i = 1; i < n; i++) { // 对所有边 松弛 n-1 次
for (vector<int> &side : grid) { // 每一次松弛,都是对所有边进行松弛
int from = side[0]; // 边的出发点
int to = side[1]; // 边的到达点
int price = side[2]; // 边的权值
// 松弛操作
// minDist[from] != INT_MAX 防止从未计算过的节点出发
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) {
minDist[to] = minDist[from] + price;
}
}
}
if (minDist[end] == INT_MAX) cout << "unconnected" << endl; // 不能到达终点
else cout << minDist[end] << endl; // 到达终点最短路径
}
Bellman_ford 算法每次松弛 都是对所有边进行松弛。但真正有效的松弛,是基于已经计算过的节点在做的松弛。对上一次松弛的时候更新过的节点作为出发节点所连接的边 进行松弛就够了1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
using namespace std;
struct Edge { //邻接表
int to; // 链接的节点
int val; // 边的权重
Edge(int t, int w): to(t), val(w) {} // 构造函数
};
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<list<Edge>> grid(n + 1);
vector<bool> isInQueue(n + 1); // 加入优化,已经在队里里的元素不用重复添加
// 将所有边保存起来
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2,权值为 val
grid[p1].push_back(Edge(p2, val));
}
int start = 1; // 起点
int end = n; // 终点
vector<int> minDist(n + 1 , INT_MAX);
minDist[start] = 0;
queue<int> que;
que.push(start);
while (!que.empty()) {
int node = que.front(); que.pop();
isInQueue[node] = false; // 从队列里取出的时候,要取消标记,我们只保证已经在队列里的元素不用重复加入
for (Edge edge : grid[node]) {
int from = node;
int to = edge.to;
int value = edge.val;
if (minDist[to] > minDist[from] + value) { // 开始松弛
minDist[to] = minDist[from] + value;
if (isInQueue[to] == false) { // 已经在队列里的元素不用重复添加
que.push(to);
isInQueue[to] = true;
}
}
}
}
if (minDist[end] == INT_MAX) cout << "unconnected" << endl; // 不能到达终点
else cout << minDist[end] << endl; // 到达终点最短路径
}
判断负权回路与计算有限最短路
在没有负权回路的图中,松弛 n 次以上 ,结果不会有变化。
但有负权回路,如果松弛 n 次,结果就会有变化了,因为 有负权回路 就是可以无限最短路径(一直绕圈,就可以一直得到无限小的最短距离)。 也就是说在进行最后一次松弛时如果也进行了更新,表明有负权回路1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
using namespace std;
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<vector<int>> grid;
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
// p1 指向 p2,权值为 val
grid.push_back({p1, p2, val});
}
int start = 1; // 起点
int end = n; // 终点
vector<int> minDist(n + 1 , INT_MAX);
minDist[start] = 0;
bool flag = false;
for (int i = 1; i <= n; i++) { // 这里我们松弛n次,最后一次判断负权回路
for (vector<int> &side : grid) {
int from = side[0];
int to = side[1];
int price = side[2];
if (i < n) {
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) minDist[to] = minDist[from] + price;
} else { // 多加一次松弛判断负权回路
if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) flag = true;
}
}
}
if (flag) cout << "circle" << endl;
else if (minDist[end] == INT_MAX) {
cout << "unconnected" << endl;
} else {
cout << minDist[end] << endl;
}
}
对所有边松弛了n-1次后,在松弛一次,如果出现minDist出现变化就判断有负权回路。
如果使用 SPFA 那么节点都是进队列的,如果节点加入队列的次数 超过了 n-1次 ,那么该图就一定有负权回路。
在单源有限路径下,也就最多经过 k 个节点的条件下,而不是一定经过k个节点,也可以经过的节点数量比k小,但要最短的路径。对所有边松弛一次,相当于计算 起点到达与起点一条边相连的节点 的最短距离,那么对所有边松弛 k + 1次,就是求 起点到达 与起点k + 1条边相连的节点的 最短距离。
理论上来说,对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离。
对所有边松弛两次,相当于计算 起点到达 与起点两条边相连的节点的最短距离。
对所有边松弛三次,以此类推。但在对所有边松弛第一次的过程中,会发现,不仅仅 与起点一条边相连的节点更新了,所有节点都更新了。而且对所有边的后面几次松弛,同样是更新了所有的节点,说明 至多经过k 个节点 这个限制 根本没有限制住,每个节点的数值都被更新了。
计算minDist数组的时候,基于了本次松弛的 minDist数值,而不是上一次 松弛时候minDist的数值。
所以在每次计算 minDist 时候,要基于对所有边上一次松弛的 minDist 数值才行,所以我们要记录上一次松弛的minDist。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
using namespace std;
int main() {
int src, dst,k ,p1, p2, val ,m , n;
cin >> n >> m;
vector<vector<int>> grid;
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
grid.push_back({p1, p2, val});
}
cin >> src >> dst >> k;
vector<int> minDist(n + 1 , INT_MAX);
minDist[src] = 0;
vector<int> minDist_copy(n + 1); // 用来记录上一次遍历的结果
for (int i = 1; i <= k + 1; i++) {
minDist_copy = minDist; // 获取上一次计算的结果
for (vector<int> &side : grid) {
int from = side[0];
int to = side[1];
int price = side[2];
// 注意使用 minDist_copy 来计算 minDist
if (minDist_copy[from] != INT_MAX && minDist[to] > minDist_copy[from] + price) {
minDist[to] = minDist_copy[from] + price;
}
}
}
if (minDist[dst] == INT_MAX) cout << "unreachable" << endl; // 不能到达终点
else cout << minDist[dst] << endl; // 到达终点最短路径
}
多源最短路径 Floyd算法
Floyd 算法对边的权值正负没有要求,都可以处理
遍历k 的for循环一定是在最外面,这样才能一层一层去遍历1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
using namespace std;
int main() {
int n, m, p1, p2, val;
cin >> n >> m;
vector<vector<int>> grid(n + 1, vector<int>(n + 1, 10005)); // 因为边的最大距离是10^4
for(int i = 0; i < m; i++){
cin >> p1 >> p2 >> val;
grid[p1][p2] = val;
grid[p2][p1] = val; // 注意这里是双向图
}
// 开始 floyd
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
grid[i][j] = min(grid[i][j], grid[i][k] + grid[k][j]);
}
}
}
// 输出结果
int z, start, end;
cin >> z;
while (z--) {
cin >> start >> end;
if (grid[start][end] == 10005) cout << -1 << endl;
else cout << grid[start][end] << endl;
}
}
using namespace std;
int main() {
int n,m;
cin>>n>>m;
// grid[i][j][k] 表示i到j经过k的最小值
// vector<vector<vector<int>>> grid(n+1,vector<vector<int>>(n+1,vector<int>(n+1,10001)));
vector<vector<int>> grid(n+1,vector<int>(n+1,INT_MAX));
while(m--) {
int u,v,w;
cin>>u>>v>>w;
grid[u][v] = w;
grid[v][u] = w;
grid[v][v] = 0;
grid[u][u] = 0;
}
for(int k = 1;k<=n;k++) {
for(int i = 1;i<=n;i++) {
for(int j = 1;j<=n;j++) {
if(grid[i][k] == INT_MAX || grid[k][j] == INT_MAX) {
continue;
}
if(grid[i][j]>grid[i][k]+grid[k][j]) {
grid[i][j]=grid[i][k]+grid[k][j];
}
}
}
}
int Q;
cin>>Q;
while(Q--) {
int s,t;
cin>>s>>t;
if(grid[s][t] == INT_MAX) {
cout<<-1<<endl;
}else{
cout<<grid[s][t]<<endl;
}
}
return 0;
}
最小生成树
最小生成树(Minimum Spanning Tree,简称 MST)是图论中的一个核心概念,它定义为从一个无向、连通、带权重的图中,选出一组边,使得:
- 这些边连接了图中的所有节点。
- 这些边没有形成任何环。
- 所有边的权重总和最小。
简单来说,如果把一个图看作是城市和连接它们的道路,每条道路都有建设成本,那么最小生成树就是用最低的总成本,将所有城市连接起来的最经济的道路网络
Prim
prim算法是从节点的角度采用贪心的策略每次寻找距离最小生成树最近的节点并加入到最小生成树中。
prim算法核心就是三步,我称为prim三部曲,大家一定要熟悉这三步,代码相对会好些很多:
- 第一步,选距离生成树最近节点
- 第二步,最近节点加入生成树
- 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
1 |
|
Kruskal
prim 算法是维护节点的集合,而 Kruskal 是维护边的集合
kruscal的思路:
- 边的权值排序,因为要优先选最小的边加入到生成树里
- 遍历排序后的边
- 如果边首尾的两个节点在同一个集合,说明如果连上这条边图中会出现环
- 如果边首尾的两个节点不在同一个集合,加入到最小生成树,并把两个节点加入同一个集合
1 |
|
并查集
拓扑排序
时间复杂度
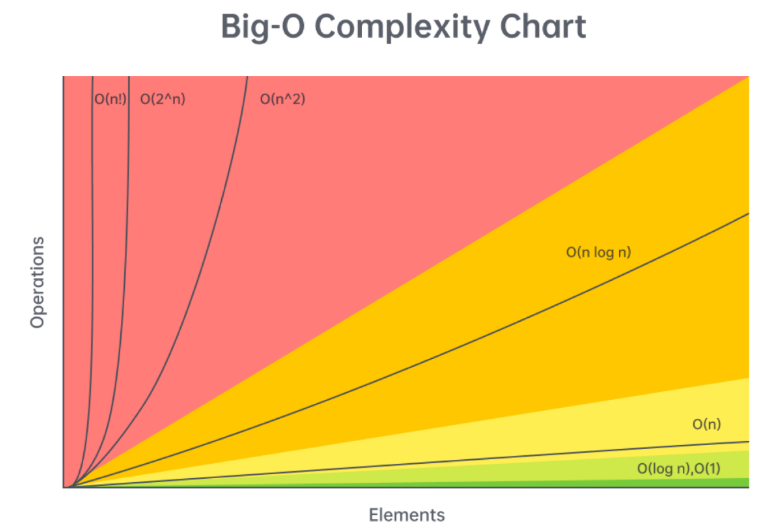
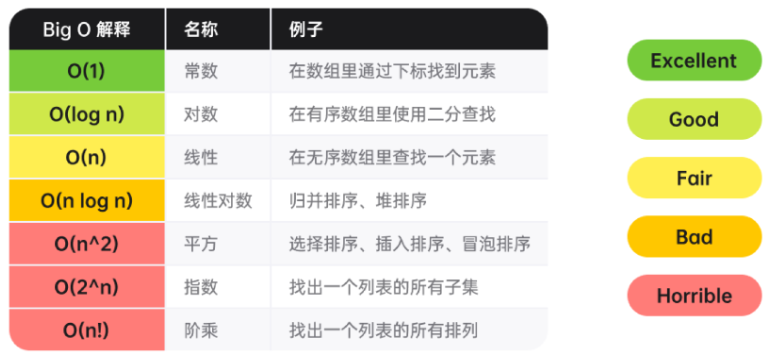
常见数据结构操作时间复杂度
数组

字符串

链表

哈希表/字典

集合

栈

队列

二叉树问题

二叉搜索树

堆/优先队列

二分查找
在最坏的情况下,二分查找的时间复杂度为 O(logn,其中 nn 是初始搜索空间的大小。
其他


输入大小与时间复杂度
问题的约束可以被视为提示,因为它们指示解决方案时间复杂度的上限。能够在给定输入大小的情况下计算出解决方案的预期时间复杂度是一项宝贵的技能。



排序算法

